Jess 是加州大学伯克利分校的博士生,她通过将机器学习中的概率模型与认知科学中的行为实验相结合来研究人类认知。在业余时间,Jess 是 IPython 和 Jupyter 的核心贡献者。她还拥有麻省理工学院的计算机科学学士学位和硕士学位。
在计算机科学和工程领域,我们经常遇到无法用方程式解决的问题。这些问题通常涉及复杂系统、噪声输入或两者兼而有之。以下只是一些现实世界中没有精确解析解的问题的示例
您已经建立了飞机的计算机模型,并且想要确定飞机在不同天气条件下的承受能力。
您想要确定基于地下水扩散模型,拟建工厂的化学物质径流是否会影响附近居民的供水。
您有一台机器人,它从相机捕捉到噪声图像,并且想要恢复这些图像所描绘的物体的三维结构。
您想要计算如果您采取特定动作,您在国际象棋比赛中获胜的可能性。
即使这些类型的问题无法精确解决,我们通常可以通过称为 *蒙特卡洛采样* 方法的技术来获得它们的近似解。在蒙特卡罗方法中,关键思想是获取许多 *样本*,这将使您能够估计解决方案。1
术语 *采样* 表示从某个概率分布中生成随机值。例如,您从掷六面骰子得到的数值就是一个样本。在洗牌后从牌堆顶端抽取的牌就是一个样本。飞镖击中靶盘的位置也是一个样本。这些不同样本之间的唯一区别是它们是从不同的 *概率分布* 生成的。在骰子的情况下,该分布在六个值上分配了相同的权重。在牌的情况下,该分布在 52 个值上分配了相同的权重。在飞镖靶盘的情况下,该分布在圆形区域上分配了权重(尽管它可能不是均匀分布,具体取决于您作为飞镖玩家的技巧)。
通常我们希望通过两种方式使用样本。第一个只是生成一个随机值,以便稍后使用:例如,在扑克的电脑游戏中随机抽牌。样本使用的第二种方式是进行估计。例如,如果您怀疑您的朋友正在玩作弊骰子,您可能想要掷很多次骰子,看看某些数字出现的频率是否比您预期的高。或者,您可能只是想要描述可能的范围,例如上面的飞机示例。天气是一个相当混乱的系统,这意味着无法精确计算飞机是否会在特定天气状况下幸存下来。相反,您可以模拟飞机在许多不同天气条件下的行为,多次,这将使您能够了解在哪些条件下飞机最有可能发生故障。
与计算机科学中的大多数应用程序一样,在使用样本和概率进行编程时,您可以做出设计决策,这些决策将影响代码的整体整洁性、连贯性和正确性。在本章中,我们将通过一个简单的示例来介绍如何在电脑游戏中随机采样项目。特别是,我们将重点介绍与概率处理相关的设计决策,包括用于采样和评估概率的函数、与对数的交互、允许可重复性以及将生成样本的过程与特定应用程序分开。
我们将使用像 \(p(x)\) 这样的数学符号来表示 \(p\) 是随机变量的 *概率密度函数* (PDF) 或 *概率质量函数* (PMF),在值 \(x\) 上。PDF 是一个 *连续* 函数 \(p(x)\),使得 \(\int_{-\infty}^\infty p(x)\ \mathrm{d}x=1\),而 PMF 是一个 *离散* 函数 \(p(x)\),使得 \(\sum_{x\in \mathbb{Z}} p(x)=1\),其中 \(\mathbb{Z}\) 是所有整数的集合。
在飞镖靶盘的情况下,概率分布将是一个连续的 PDF,而在骰子的情况下,概率分布将是一个离散的 PMF。在这两种情况下,\(p(x) \geq 0\) 对于所有 \(x\);即概率必须是非负的。
我们可能希望对概率分布做两件事。给定一个值(或位置)\(x\),我们可能想要 *评估* 该位置的概率密度(或质量)。在数学符号中,我们将用 \(p(x)\) 表示(值 \(x\) 的概率密度)。
给定 PDF 或 PMF,我们也可能想要 *采样* 一个值 \(x\),以与分布成比例的方式(这样我们更有可能在概率更高的位置获得样本)。在数学符号中,我们将用 \(x\sim p\) 表示,表示 \(x\) 是按比例于 \(p\) 采样的。
为了简单起见,我们以一个简单的例子来演示与概率编程相关的各种设计决策,假设我们要编写一个角色扮演游戏(RPG)。我们希望有一种方法来生成怪物随机掉落的魔法物品的奖励属性。我们可能决定我们想要物品授予的最大奖励是 +5,并且较高的奖励比较低的奖励的可能性更低。如果 \(B\) 是奖励值的随机变量,那么
\[ p(B=\mathrm{+1}) = 0.55\\ p(B=\mathrm{+2}) = 0.25\\ p(B=\mathrm{+3}) = 0.12\\ p(B=\mathrm{+4}) = 0.06\\ p(B=\mathrm{+5}) = 0.02 \]
我们还可以指定我们的奖励应该分配到六个属性(敏捷、体质、力量、智力、智慧和魅力)中。因此,一个具有 +5 奖励的物品可以将这些点数分配到不同的属性中(例如,+2 智慧和 +3 智力),也可以集中在一个属性中(例如,+5 魅力)。
我们如何从该分布中随机采样?最简单的方法可能是首先采样整体物品奖励,然后采样奖励在属性中的分配方式。方便的是,奖励和奖励分配方式的概率分布都是 *多项分布* 的实例。
当您有多个可能的输出,并且想要描述每个输出发生的概率时,使用多项分布。用于解释多项分布的经典示例是 *球和瓮*。想法是您有一个瓮,其中包含不同颜色的球(例如,30% 红色、20% 蓝色和 50% 绿色)。您取出一个球,记录其颜色,然后放回瓮中,然后重复此操作多次。在这种情况下,*输出* 对应于绘制特定颜色的球,并且每个输出的概率对应于该颜色球的比例(例如,对于绘制蓝球的输出,概率为 \(p(\mathrm{blue})=0.20\))。然后,多项分布用于描述在绘制多个球时可能出现的输出组合(例如,两个绿色球和一个蓝色球)。
本节中的代码位于文件 multinomial.py 中。
MultinomialDistribution 类一般来说,分布有两个用例:我们可能想要从该分布中 *采样*,并且我们可能想要 *评估* 该分布的 PMF 或 PDF 下的样本(或样本)的概率。虽然执行这两个函数所需的实际计算相当不同,但它们依赖于一个共同的信息:分布的 *参数* 是什么。在多项分布的情况下,参数是事件概率 \(p\)(对应于上述瓮示例中不同颜色球的比例)。
最简单的解决方案可能是简单地创建两个函数,这两个函数都采用相同的参数,但除此之外是独立的。但是,我通常会选择使用类来表示我的分布。这样做有几个优点
在实践中,这是许多统计软件包的工作原理,包括 SciPy 自己的分布,它们位于 scipy.stats 模块中。但是,我们虽然使用了其他 SciPy 函数,但没有使用它们的概率分布,既是为了说明,也是因为 SciPy 目前还没有多项分布。
以下是类的构造函数代码
import numpy as np
class MultinomialDistribution(object):
def __init__(self, p, rso=np.random):
"""Initialize the multinomial random variable.
Parameters
----------
p: numpy array of length `k`
The event probabilities
rso: numpy RandomState object (default: None)
The random number generator
"""
# Check that the probabilities sum to 1. If they don't, then
# something is wrong! We use `np.isclose` rather than checking
# for exact equality because in many cases, we won't have
# exact equality due to floating-point error.
if not np.isclose(np.sum(p), 1.0):
raise ValueError("event probabilities do not sum to 1")
# Store the parameters that were passed in
self.p = p
self.rso = rso
# Precompute log probabilities, for use by the log-PMF, for
# each element of `self.p` (the function `np.log` operates
# elementwise over NumPy arrays, as well as on scalars.)
self.logp = np.log(self.p)该类以事件概率 \(p\) 和一个名为 rso 的变量作为参数。首先,构造函数检查参数是否有效;即 p 的总和为 1。然后它存储传入的参数,并使用事件概率来计算事件 *对数* 概率。(我们稍后将讨论为什么要这样做)。rso 对象是我们稍后用于生成随机数的对象。(稍后我们将详细讨论它是什么)。
在我们深入研究类的其余部分之前,让我们回顾与构造函数相关的两个要点。
通常,鼓励程序员使用描述性变量名:例如,使用名称 independent_variable 和 dependent_variable 比使用 x 和 y 更好。一个标准的经验法则是永远不要使用只有一两个字符的变量名。但是,您会注意到,在我们的 MultinomialDistribution 类的构造函数中,我们使用了变量名 p,这违反了典型的命名约定。
虽然我同意这种命名约定应该适用于几乎所有领域,但有一个例外:数学。将数学方程编码成代码的难度在于这些方程通常具有仅用一个字母表示的变量名:\(x\)、\(y\)、\(\alpha\) 等。因此,如果您将它们直接翻译成代码,最简单的变量名将是 x、y 和 alpha。显然,这些不是最有信息的变量名(名称 x 没有传达太多信息),但使用更具描述性的变量名也会使在代码和方程之间切换变得更加困难。
我认为,当您编写直接实现方程式的代码时,应该使用与方程式中相同的变量名。这样可以很容易地看到代码的哪些部分在实现方程式的哪些部分。当然,这可能会使代码在孤立的情况下难以理解,因此,注释解释各种计算的目标就显得尤为重要。如果方程式在学术论文中列出,注释应引用方程式编号,以便可以轻松查找。
您可能已经注意到,我们将 numpy 模块导入为 np。这是数值计算领域中的标准做法,因为 NumPy 提供了大量有用的函数,其中许多函数即使在一个文件中也可能被使用。在本节的简单示例中,我们只使用了 11 个 NumPy 函数,但数量可能要高得多:我经常在一个项目中使用大约 40 个不同的 NumPy 函数!
导入 NumPy 有几种选择。我们可以使用 from numpy import *,但这通常是糟糕的风格,因为它难以确定函数来自何处。我们可以单独导入函数,例如 from numpy import array, log, ...,但这很快就会变得笨拙。我们也可以只使用 import numpy,但这会导致代码难以阅读。以下两个示例都很难阅读,但使用 np 而不是 numpy 的示例明显更清晰
>>> numpy.sqrt(numpy.sum(numpy.dot(numpy.array(a), numpy.array(b))))
>>> np.sqrt(np.sum(np.dot(np.array(a), np.array(b))))从多项式分布中采样实际上相当简单,因为 NumPy 为我们提供了执行此操作的函数:np.random.multinomial2.
尽管此函数已经存在,但我们仍然可以围绕它做出一些设计决策。
虽然我们确实想要绘制一个随机样本,但有时我们希望结果是可复制的:即使数字看起来是随机的,如果我们再次运行程序,我们可能希望它使用相同的“随机”数序列。
为了允许生成这样的“可复制随机”数,我们需要告诉我们的采样函数如何生成随机数。我们可以通过使用 NumPy RandomState 对象来实现这一点,该对象本质上是一个随机数生成器对象,可以传递。它拥有与 np.random 大致相同的函数;不同之处在于我们可以控制随机数的来源。我们按如下方式创建它
>>> import numpy as np
>>> rso = np.random.RandomState(230489)其中传递给 RandomState 构造函数的数字是随机数生成器的种子。只要我们用相同的种子实例化它,RandomState 对象就会按相同顺序生成相同的“随机”数,从而确保可复制性
>>> rso.rand()
0.5356709186237074
>>> rso.rand()
0.6190581888276206
>>> rso.rand()
0.23143573416770336
>>> rso.seed(230489)
>>> rso.rand()
0.5356709186237074
>>> rso.rand()
0.6190581888276206之前我们看到构造函数接受一个名为 rso 的参数。这个 rso 变量是一个已经初始化的 RandomState 对象。我喜欢将 RandomState 对象设为可选参数:有时不必强制使用它很方便,但我确实希望有使用它的选项(如果我仅使用 np.random 模块,我将无法做到这一点)。
因此,如果未给出 rso 变量,则构造函数将默认为 np.random.multinomial。否则,它将使用来自 RandomState 对象本身的多项式采样器3.
一旦我们决定是否使用 np.random.multinomial 或 rso.multinomial,采样就只是一个调用相应函数的问题。但是,我们可能会考虑另一个决定:什么算作参数?
之前我说结果概率 \(p\) 是多项式分布的参数。但是,根据你问的是谁,事件数量 \(n\) 也可以是多项式分布的参数。那么,为什么我们没有将 \(n\) 作为构造函数的参数呢?
这个问题虽然与多项式分布比较具体,但实际上在处理概率分布时经常出现,答案实际上取决于用例。对于多项式,你能否假设事件数量始终相同?如果是,那么最好将 \(n\) 作为构造函数的参数传递。如果不是,那么要求在对象创建时指定 \(n\) 会非常严格,甚至可能要求你每次需要抽取样本时都创建一个新的分布对象!
我通常不喜欢被代码限制得太死,因此选择将 n 作为 sample 函数的参数,而不是将其作为构造函数的参数。另一种解决方案可能是将 n 作为构造函数的参数,但同时包含允许更改 n 值的方法,而无需创建全新的对象。但是,对于我们的目的,这种解决方案可能太过复杂,因此我们将坚持将其作为 sample 的参数
def sample(self, n):
"""Samples draws of `n` events from a multinomial distribution with
outcome probabilities `self.p`.
Parameters
----------
n: integer
The number of total events
Returns
-------
numpy array of length `k`
The sampled number of occurrences for each outcome
"""
x = self.rso.multinomial(n, self.p)
return x虽然我们没有明确地需要计算我们生成的魔法物品的概率,但编写一个可以计算分布的概率质量函数 (PMF) 或概率密度函数 (PDF) 的函数几乎总是好的。为什么?
一个原因是我们可以用它进行测试:如果我们使用我们的采样函数进行多次采样,那么它们应该近似于精确的 PDF 或 PMF。如果经过多次采样后,近似值很差或明显错误,那么我们就知道了我们的代码中存在错误。
实现 PMF 或 PDF 的另一个原因是,你经常会在以后的某个时间点实际需要它,但最初并没有意识到。例如,我们可能希望根据我们生成它们的可能性对我们随机生成的项目进行分类,例如常见、不常见和稀有。要确定这一点,我们需要能够计算 PMF。
最后,在许多情况下,你的具体用例会决定你从一开始就实现 PMF 或 PDF。
正式地说,多项式分布具有以下方程
\[ p(\mathbf{x}; \mathbf{p}) = \frac{(\sum_{i=1}^k x_i)!}{x_1!\cdots{}x_k!}p_1^{x_1}\cdots{}p_k^{x_k} \]
其中 \(\mathbf{x}=[x_1, \ldots{}, x_k]\) 是一个长度为 \(k\) 的向量,指定每个事件发生的次数,\(\mathbf{p}=[p_1, \ldots{}, p_k]\) 是一个向量,指定每个事件发生的概率。如上所述,事件概率 \(\mathbf{p}\) 是分布的参数。
上述方程中的阶乘实际上可以使用一个特殊的函数 \(\Gamma\) 表示,称为伽马函数。当我们开始编写代码时,使用伽马函数而不是阶乘会更加方便和高效,因此我们将使用 \(\Gamma\) 重新编写方程
\[ p(\mathbf{x}; \mathbf{p}) = \frac{\Gamma((\sum_{i=1}^k x_i)+1)}{\Gamma(x_1+1)\cdots{}\Gamma(x_k+1)}p_1^{x_1}\cdots{}p_k^{x_k} \]
在深入研究实际实现上述方程所需的代码之前,我想强调在编写包含概率的代码时最重要的设计决策之一:使用对数值。这意味着,我们不应该直接使用概率 \(p(x)\),而应该使用对数概率 \(\log{p(x)}\)。这是因为概率可以很快变得非常小,从而导致下溢错误。
为了说明这一点,请考虑概率必须介于 0 和 1 之间(包括)。NumPy 具有一个有用的函数 finfo,它将告诉我们系统中浮点值的限制。例如,在 64 位机器上,我们看到最小的可用正数(由 tiny 给出)是
>>> import numpy as np
>>> np.finfo(float).tiny
2.2250738585072014e-308虽然这似乎非常小,但遇到这种数量级甚至更小的概率并不少见。此外,将概率相乘是一个常见的操作,但是如果我们尝试用非常小的概率进行此操作,我们就会遇到下溢问题
>>> tiny = np.finfo(float).tiny
>>> # if we multiply numbers that are too small, we lose all precision
>>> tiny * tiny
0.0但是,取对数可以帮助缓解这个问题,因为我们可以用对数表示比平时更广泛的数字范围。正式地说,对数值范围从 \(-\infty\) 到零。在实践中,它们范围从 finfo 返回的 min 值(可以表示的最小数字)到零。min 值远远小于 tiny 值的对数(如果我们不使用对数空间,这将是我们的下界)
>>> # this is our lower bound normally
>>> np.log(tiny)
-708.39641853226408
>>> # this is our lower bound when using logs
>>> np.finfo(float).min
-1.7976931348623157e+308因此,通过使用对数值,我们可以极大地扩展我们可表示的数字范围。此外,我们可以使用加法对对数进行乘法运算,因为 \(\log(x\cdot{}y) = \log(x) + \log(y)\)。因此,如果我们对对数进行上述乘法运算,我们就不必担心(太多)由于下溢而导致精度丢失
>>> # the result of multiplying small probabilities
>>> np.log(tiny * tiny)
-inf
>>> # the result of adding small log probabilities
>>> np.log(tiny) + np.log(tiny)
-1416.7928370645282当然,这种解决方案不是万能药。如果我们需要从对数中推导出数字(例如,要添加概率而不是将它们相乘),那么我们又回到了下溢
>>> tiny*tiny
0.0
>>> np.exp(np.log(tiny) + np.log(tiny))
0.0尽管如此,对所有计算进行对数运算可以节省很多麻烦。如果我们需要返回原始数字,我们可能不得不失去这种精度,但我们至少保留了有关概率的一些信息(足以比较它们,例如)——否则这些信息会丢失。
现在我们已经看到了使用对数的重要性,我们可以实际编写函数来计算对数-PMF
def log_pmf(self, x):
"""Evaluates the log-probability mass function (log-PMF) of a
multinomial with outcome probabilities `self.p` for a draw `x`.
Parameters
----------
x: numpy array of length `k`
The number of occurrences of each outcome
Returns
-------
The evaluated log-PMF for draw `x`
"""
# Get the total number of events
n = np.sum(x)
# equivalent to log(n!)
log_n_factorial = gammaln(n + 1)
# equivalent to log(x1! * ... * xk!)
sum_log_xi_factorial = np.sum(gammaln(x + 1))
# If one of the values of self.p is 0, then the corresponding
# value of self.logp will be -inf. If the corresponding value
# of x is 0, then multiplying them together will give nan, but
# we want it to just be 0.
log_pi_xi = self.logp * x
log_pi_xi[x == 0] = 0
# equivalent to log(p1^x1 * ... * pk^xk)
sum_log_pi_xi = np.sum(log_pi_xi)
# Put it all together
log_pmf = log_n_factorial - sum_log_xi_factorial + sum_log_pi_xi
return log_pmf在大多数情况下,这是上述多项式 PMF 方程的直接实现。gammaln 函数来自 scipy.special,并计算对数-伽马函数 \(\log{\Gamma(x)}\)。如上所述,使用伽马函数而不是阶乘函数更方便;这是因为 SciPy 为我们提供了一个对数-伽马函数,但没有提供对数-阶乘函数。我们可以自己计算一个对数阶乘,例如
log_n_factorial = np.sum(np.log(np.arange(1, n + 1)))
sum_log_xi_factorial = np.sum([np.sum(np.log(np.arange(1, i + 1))) for i in x])但如果使用 SciPy 中内置的伽马函数,更容易理解、更容易编写代码,而且计算效率更高。
我们需要解决一个边缘情况:当我们的概率之一为零时。当 \(p_i=0\) 时,则 \(\log{p_i}=-\infty\)。这很好,除了当无穷大乘以零时,会出现以下行为
>>> # it's fine to multiply infinity by integers...
>>> -np.inf * 2.0
-inf
>>> # ...but things break when we try to multiply by zero
>>> -np.inf * 0.0
nannan 表示“非数字”,并且几乎总是很难处理,因为大多数与 nan 的计算会导致另一个 nan。因此,如果我们不处理 \(p_i=0\) 且 \(x_i=0\) 的情况,最终会得到一个 nan。它将与其他数字相加,生成另一个 nan,这根本没有用。为了处理这种情况,我们专门检查 \(x_i=0\) 的情况,并将由此产生的 \(x_i\cdot{}\log(p_i)\) 也设置为零。
让我们再回到我们关于使用对数的讨论。即使我们实际上只需要 PMF 而不是对数-PMF,也通常最好先用对数计算它,然后如果需要,再对其求幂
def pmf(self, x):
"""Evaluates the probability mass function (PMF) of a multinomial
with outcome probabilities `self.p` for a draw `x`.
Parameters
----------
x: numpy array of length `k`
The number of occurrences of each outcome
Returns
-------
The evaluated PMF for draw `x`
"""
pmf = np.exp(self.log_pmf(x))
return pmf为了进一步强调使用对数的重要性,我们可以看一个只使用多项式的示例
>>> dist = MultinomialDistribution(np.array([0.25, 0.25, 0.25, 0.25]))
>>> dist.log_pmf(np.array([1000, 0, 0, 0])
-1386.2943611198905
>>> dist.log_pmf(np.array([999, 0, 0, 0])
-1384.9080667587707在这种情况下,我们得到极小的概率(你会注意到,这些概率比我们上面讨论的tiny值要小得多)。这是因为 PMF 中的分数非常大:1000 的阶乘甚至无法计算,因为会发生溢出。但是,阶乘的对数是可以计算的。
>>> from scipy.special import gamma, gammaln
>>> gamma(1000 + 1)
inf
>>> gammaln(1000 + 1)
5912.1281784881639如果我们尝试使用gamma函数仅计算 PMF,最终将得到gamma(1000 + 1) / gamma(1000 + 1),这将导致nan值(即使我们可以看到它应该是 1)。但是,由于我们使用对数进行计算,所以这并不成问题,我们不必担心它!
现在我们已经编写了多项式函数,我们可以将它们用于生成我们的魔法物品。为此,我们将创建一个名为MagicItemDistribution的类,它位于rpg.py文件中。
class MagicItemDistribution(object):
# these are the names (and order) of the stats that all magical
# items will have
stats_names = ("dexterity", "constitution", "strength",
"intelligence", "wisdom", "charisma")
def __init__(self, bonus_probs, stats_probs, rso=np.random):
"""Initialize a magic item distribution parameterized by `bonus_probs`
and `stats_probs`.
Parameters
----------
bonus_probs: numpy array of length m
The probabilities of the overall bonuses. Each index in
the array corresponds to the bonus of that amount (e.g.,
index 0 is +0, index 1 is +1, etc.)
stats_probs: numpy array of length 6
The probabilities of how the overall bonus is distributed
among the different stats. `stats_probs[i]` corresponds to
the probability of giving a bonus point to the ith stat;
i.e., the value at `MagicItemDistribution.stats_names[i]`.
rso: numpy RandomState object (default: np.random)
The random number generator
"""
# Create the multinomial distributions we'll be using
self.bonus_dist = MultinomialDistribution(bonus_probs, rso=rso)
self.stats_dist = MultinomialDistribution(stats_probs, rso=rso)我们的MagicItemDistribution类的构造函数接受奖励概率、属性概率和随机数生成器的参数。尽管我们在上面指定了我们希望奖励概率是什么,但通常将参数编码为传递进来的参数是一个好主意。这为在不同分布下对物品进行抽样提供了可能性。(例如,奖励概率可能会随着玩家等级的提高而改变。)我们将属性的名称编码为类变量stats_names,尽管这也可以很容易地作为构造函数的另一个参数。
如前所述,抽取魔法物品有两个步骤:首先抽取总奖励,然后抽取奖励在属性上的分布。因此,我们将这些步骤编码为两种方法:_sample_bonus和_sample_stats
def _sample_bonus(self):
"""Sample a value of the overall bonus.
Returns
-------
integer
The overall bonus
"""
# The bonus is essentially just a sample from a multinomial
# distribution with n=1; i.e., only one event occurs.
sample = self.bonus_dist.sample(1)
# `sample` is an array of zeros and a single one at the
# location corresponding to the bonus. We want to convert this
# one into the actual value of the bonus.
bonus = np.argmax(sample)
return bonus
def _sample_stats(self):
"""Sample the overall bonus and how it is distributed across the
different stats.
Returns
-------
numpy array of length 6
The number of bonus points for each stat
"""
# First we need to sample the overall bonus
bonus = self._sample_bonus()
# Then, we use a different multinomial distribution to sample
# how that bonus is distributed. The bonus corresponds to the
# number of events.
stats = self.stats_dist.sample(bonus)
return stats我们可以将它们合并为一个方法——尤其是因为_sample_stats是唯一依赖_sample_bonus的函数——但我选择将它们分开,既是因为它使抽样程序更容易理解,也是因为将其分解为更小的部分使代码更容易测试。
你还会注意到这些方法前面有一个下划线,表明它们不是真的要用于类之外。相反,我们提供函数sample
def sample(self):
"""Sample a random magical item.
Returns
-------
dictionary
The keys are the names of the stats, and the values are
the bonus conferred to the corresponding stat.
"""
stats = self._sample_stats()
item_stats = dict(zip(self.stats_names, stats))
return item_statssample函数的功能与_sample_stats基本相同,只是它返回一个字典,字典中属性的名称作为键。这为抽样物品提供了一个简洁易懂的接口——很明显哪些属性有多少奖励点数——但也保留了只使用_sample_stats的选项,如果需要进行多次抽样且需要效率的话。
我们对评估物品的概率使用类似的设计。同样,我们公开了高级方法pmf和log_pmf,它们接受由sample生成的格式的字典
def log_pmf(self, item):
"""Compute the log probability of the given magical item.
Parameters
----------
item: dictionary
The keys are the names of the stats, and the values are
the bonuses conferred to the corresponding stat.
Returns
-------
float
The value corresponding to log(p(item))
"""
# First pull out the bonus points for each stat, in the
# correct order, then pass that to _stats_log_pmf.
stats = np.array([item[stat] for stat in self.stats_names])
log_pmf = self._stats_log_pmf(stats)
return log_pmf
def pmf(self, item):
"""Compute the probability the given magical item.
Parameters
----------
item: dictionary
The keys are the names of the stats, and the values are
the bonus conferred to the corresponding stat.
Returns
-------
float
The value corresponding to p(item)
"""
return np.exp(self.log_pmf(item))这些方法依赖于_stats_log_pmf,它计算属性的概率(但它接受一个数组而不是一个字典)
def _stats_log_pmf(self, stats):
"""Evaluate the log-PMF for the given distribution of bonus points
across the different stats.
Parameters
----------
stats: numpy array of length 6
The distribution of bonus points across the stats
Returns
-------
float
The value corresponding to log(p(stats))
"""
# There are never any leftover bonus points, so the sum of the
# stats gives us the total bonus.
total_bonus = np.sum(stats)
# First calculate the probability of the total bonus
logp_bonus = self._bonus_log_pmf(total_bonus)
# Then calculate the probability of the stats
logp_stats = self.stats_dist.log_pmf(stats)
# Then multiply them together (using addition, because we are
# working with logs)
log_pmf = logp_bonus + logp_stats
return log_pmf_stats_log_pmf方法反过来依赖于_bonus_log_pmf,它计算总奖励的概率
def _bonus_log_pmf(self, bonus):
"""Evaluate the log-PMF for the given bonus.
Parameters
----------
bonus: integer
The total bonus.
Returns
-------
float
The value corresponding to log(p(bonus))
"""
# Make sure the value that is passed in is within the
# appropriate bounds
if bonus < 0 or bonus >= len(self.bonus_dist.p):
return -np.inf
# Convert the scalar bonus value into a vector of event
# occurrences
x = np.zeros(len(self.bonus_dist.p))
x[bonus] = 1
return self.bonus_dist.log_pmf(x)我们现在可以如下创建我们的分布
>>> import numpy as np
>>> from rpg import MagicItemDistribution
>>> bonus_probs = np.array([0.0, 0.55, 0.25, 0.12, 0.06, 0.02])
>>> stats_probs = np.ones(6) / 6.0
>>> rso = np.random.RandomState(234892)
>>> item_dist = MagicItemDistribution(bonus_probs, stats_probs, rso=rso)创建后,我们可以使用它生成几个不同的物品
>>> item_dist.sample()
{'dexterity': 0, 'strength': 0, 'constitution': 0,
'intelligence': 0, 'wisdom': 0, 'charisma': 1}
>>> item_dist.sample()
{'dexterity': 0, 'strength': 0, 'constitution': 1,
'intelligence': 0, 'wisdom': 2, 'charisma': 0}
>>> item_dist.sample()
{'dexterity': 1, 'strength': 0, 'constitution': 1,
'intelligence': 0, 'wisdom': 0, 'charisma': 0}而且,如果需要,我们可以评估抽样物品的概率
>>> item = item_dist.sample()
>>> item
{'dexterity': 0, 'strength': 0, 'constitution': 0,
'intelligence': 0, 'wisdom': 2, 'charisma': 0}
>>> item_dist.log_pmf(item)
-4.9698132995760007
>>> item_dist.pmf(item)
0.0069444444444444441我们已经看到抽样的一个应用:生成怪物掉落的随机物品。我之前提到过,当你想要从整个分布中估计某样东西时,抽样也可以使用,当然,我们也有一些案例可以使用我们的MagicItemDistribution来做到这一点。例如,假设我们 RPG 中的伤害是通过掷一些数量的 D12(十二面骰子)来计算的。玩家默认可以掷一次骰子,然后根据他们的力量加成添加骰子。例如,如果他们有 +2 的力量加成,他们可以掷三个骰子。然后,造成的伤害是骰子之和。
我们可能想知道玩家在找到一定数量的武器后可以造成多少伤害;例如,作为设置怪物难度的因素。假设玩家在收集了两件物品后,希望能在大约 50% 的战斗中三击击败怪物。怪物应该有多少生命值?
解决这个问题的一种方法是通过抽样。我们可以使用以下方案
DamageDistribution 类(也位于rpg.py中)展示了该方案的实现
class DamageDistribution(object):
def __init__(self, num_items, item_dist,
num_dice_sides=12, num_hits=1, rso=np.random):
"""Initialize a distribution over attack damage. This object can
sample possible values for the attack damage dealt over
`num_hits` hits when the player has `num_items` items, and
where attack damage is computed by rolling dice with
`num_dice_sides` sides.
Parameters
----------
num_items: int
The number of items the player has.
item_dist: MagicItemDistribution object
The distribution over magic items.
num_dice_sides: int (default: 12)
The number of sides on each die.
num_hits: int (default: 1)
The number of hits across which we want to calculate damage.
rso: numpy RandomState object (default: np.random)
The random number generator
"""
# This is an array of integers corresponding to the sides of a
# single die.
self.dice_sides = np.arange(1, num_dice_sides + 1)
# Create a multinomial distribution corresponding to one of
# these dice. Each side has equal probabilities.
self.dice_dist = MultinomialDistribution(
np.ones(num_dice_sides) / float(num_dice_sides), rso=rso)
self.num_hits = num_hits
self.num_items = num_items
self.item_dist = item_dist
def sample(self):
"""Sample the attack damage.
Returns
-------
int
The sampled damage
"""
# First, we need to randomly generate items (the number of
# which was passed into the constructor).
items = [self.item_dist.sample() for i in xrange(self.num_items)]
# Based on the item stats (in particular, strength), compute
# the number of dice we get to roll.
num_dice = 1 + np.sum([item['strength'] for item in items])
# Roll the dice and compute the resulting damage.
dice_rolls = self.dice_dist.sample(self.num_hits * num_dice)
damage = np.sum(self.dice_sides * dice_rolls)
return damage构造函数接受骰子面的数量、我们要计算伤害的击数、玩家拥有的物品数量、魔法物品分布(MagicItemDistribution类型)和随机状态对象作为参数。默认情况下,我们将num_dice_sides设置为 12,因为尽管它在技术上是一个参数,但它不太可能改变。同样,我们将num_hits设置为 1 作为默认值,因为更可能的用例是我们只想对单个命中进行一次伤害样本。
然后我们在sample中实现实际的抽样逻辑。(注意它与MagicItemDistribution的结构相似性。)首先,我们生成一组玩家拥有的可能的魔法物品。然后,我们查看这些物品的力量属性,并根据这些属性计算要掷出的骰子数量。最后,我们掷骰子(再次依赖于我们可靠的多项式函数)并计算由此产生的伤害。
你可能已经注意到,我们没有在我们的DamageDistribution中包含log_pmf或pmf函数。这是因为我们实际上不知道 PMF 应该是什么!这将是等式
\[ \sum_{{item}_1, \ldots{}, {item}_m} p(\mathrm{damage} \vert \mathrm{item}_1,\ldots{},\mathrm{item}_m)p(\mathrm{item}_1)\cdots{}p(\mathrm{item}_m) \]
这个等式说的是,我们需要计算每种可能的伤害量在每种可能的 \(m\) 个物品集中的概率。我们实际上可以通过暴力计算来计算它,但这并不漂亮。这实际上是一个我们想要使用抽样来近似解决我们无法精确计算(或精确计算起来非常困难)问题的完美例子。因此,我们不会使用 PMF 方法,而是在下一节中展示如何使用许多样本近似分布。
现在我们有了机器来回答我们之前的问题:如果玩家有两件物品,并且我们希望玩家能在三击内 50% 的时间内击败怪物,那么怪物应该有多少生命值?
首先,我们创建我们的分布对象,使用之前创建的相同item_dist和rso
>>> from rpg import DamageDistribution
>>> damage_dist = DamageDistribution(2, item_dist, num_hits=3, rso=rso)现在我们可以抽取大量样本,并计算第 50 个百分位数(大于 50% 的样本的伤害值)
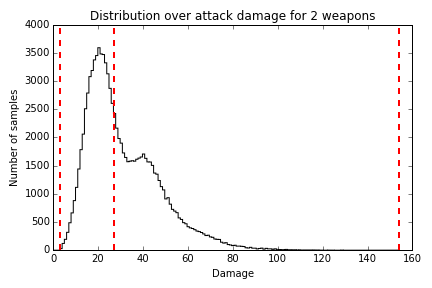
>>> samples = np.array([damage_dist.sample() for i in xrange(100000)])
>>> samples.min()
3
>>> samples.max()
154
>>> np.percentile(samples, 50)
27.0如果我们要绘制一个直方图来显示我们为每种伤害量获得的样本数量,它将看起来像图 18.1。
图 18.1 - 伤害分布
玩家可能造成的伤害范围非常大,但它有一个长尾:第 50 个百分位数为 27 点,这意味着在一半的样本中,玩家造成的伤害不超过 27 点。因此,如果我们要使用此标准来设置怪物难度,我们将给它们 27 生命值。
在本章中,我们看到了如何编写代码来从非标准概率分布中生成样本,以及如何计算这些样本的概率。在完成此示例的过程中,我们介绍了几个适用于一般情况的设计决策
MagicItemDistribution.sample的输出),同时仍然公开这些函数的不太清晰但更有效率且纯粹数值的版本(例如,MagicItemDistribution._sample_stats)。此外,我们还看到了从概率分布中抽样如何既可用于生成单个随机值(例如,在击败怪物后生成单个魔法物品),也可用于计算我们原本不知道的关于分布的信息(例如,发现拥有两件物品的玩家可能造成的伤害量)。你可能遇到的几乎所有类型的抽样都属于这两种类别之一;差异只在于你从哪些分布中抽样。代码的一般结构——独立于这些分布——保持不变。