Dessy 是一位工程师,也是一位充满激情的企业家,并且热爱开发。她目前是Nudge Rewards的首席技术官和联合创始人。当她不忙于与团队一起构建产品时,她会教授他人编程,参加或举办多伦多科技活动,并在网上发布内容,网址为dessydaskalov.com和@dess_e。
许多软件工程师在回顾他们的培训时,会记得曾经生活在一个非常理想化的世界里。我们被教导在理想化的领域中解决明确定义的问题。
然后我们被抛入了现实世界,它充满了复杂性和挑战。它很混乱,这使得它更加令人兴奋。当您能够解决现实生活中的问题,包括其所有怪癖时,您就可以构建真正帮助人们的软件。
在本章中,我们将考察一个表面上看起来很简单的问题,但当现实世界和真人被融入其中时,它会变得非常复杂。
我们将共同构建一个基本的计步器。我们将首先讨论计步器背后的理论,并在代码之外创建一个计步解决方案。然后,我们将用代码实现我们的解决方案。最后,我们将向代码添加一个 Web 层,以便用户有一个友好的界面可以使用。
让我们卷起袖子,准备解决一个现实世界中的问题。
移动设备的兴起带来了一种趋势,即收集我们日常生活中越来越多的数据。许多人收集的一种数据是他们在一段时间内走过的步数。这些数据可用于健康追踪、体育赛事训练,或者对于那些痴迷于收集和分析数据的人来说,仅仅是为了好玩。可以使用计步器来计算步数,计步器通常使用硬件加速度计的数据作为输入。
加速度计是一种测量\(x\)、\(y\)和\(z\)方向加速度的硬件。许多人无论走到哪里都会随身携带加速度计,因为它内置在目前市场上几乎所有智能手机中。\(x\)、\(y\)和\(z\)方向相对于手机。
加速度计在 3 维空间中返回一个信号。信号是在一段时间内记录的一组数据点。信号的每个分量都是一个时间序列,表示\(x\)、\(y\)或\(z\)方向之一的加速度。时间序列中的每个点都是特定时间点该方向的加速度。加速度以重力加速度单位或g来衡量。一个g等于 9.8 \(m/s^2\),即地球上平均重力加速度。
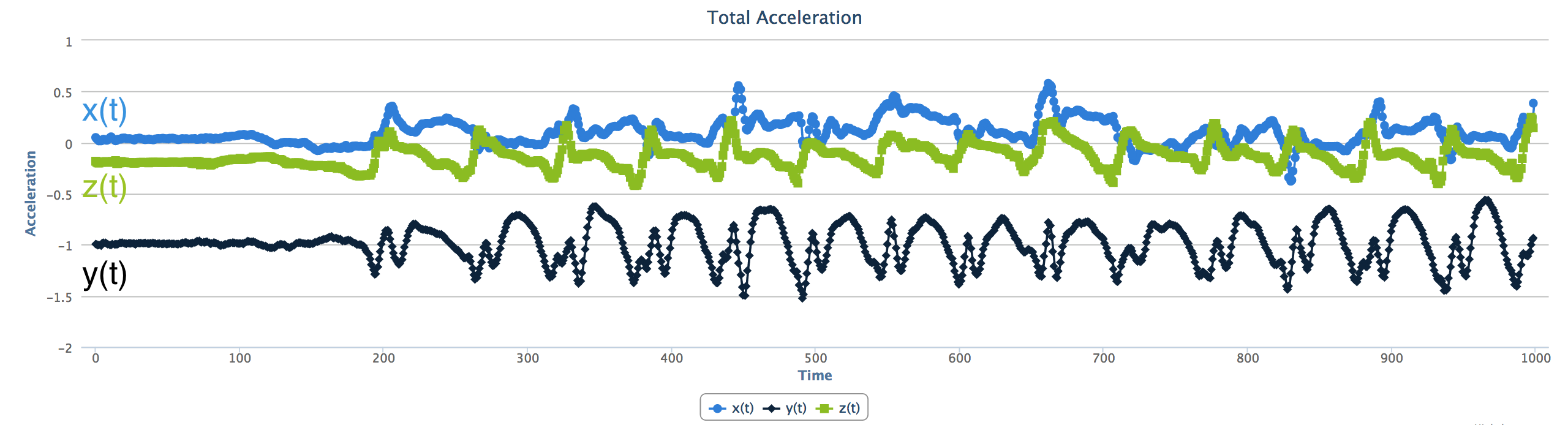
图 16.1显示了来自加速度计的示例信号,其中包含三个时间序列。
图 16.1 - 示例加速度信号
加速度计的采样率(通常可以校准)决定了每秒的测量次数。例如,采样率为 100 的加速度计每秒为每个\(x\)、\(y\)和\(z\)时间序列返回 100 个数据点。
当一个人走路时,他们会随着每一步轻微地弹跳。只需观察一个人从你身边走开时头顶的动作。他们的头部、躯干和臀部以平滑的弹跳运动同步。虽然人们弹跳的距离并不远,只有 1 或 2 厘米,但它是人行走加速度信号中最清晰、最稳定、最容易识别的部分之一。
一个人随着每一步在垂直方向上上下弹跳。如果您在地球(或另一个漂浮在太空中的大型质量球体)上行走,则弹跳会方便地与重力方向相同。
我们将通过使用加速度计来计算上下弹跳次数来计算步数。因为手机可以向任何方向旋转,所以我们将使用重力来确定哪个方向是向下。**计步器可以通过计算重力方向上的弹跳次数来计算步数。**
让我们看看一个人穿着带有加速度计的智能手机的衬衫口袋行走的情况(图 16.2)。
图 16.2 - 步行
为了简单起见,我们假设这个人
在我们的理想世界中,步弹跳产生的加速度将在\(y\)方向形成一个完美的正弦波。正弦波中的每个峰值恰好是一步。计步成为计算这些完美峰值的问题。
啊,理想世界的乐趣,我们只在这样的文本中体验过。别担心,事情即将变得更加混乱,也更加令人兴奋。让我们为我们的世界添加更多现实。
重力的作用会在重力方向产生加速度,我们称之为重力加速度。这种加速度是独一无二的,因为它始终存在,并且在本节中,它恒定为 9.8 \(m/s^2\)。
假设智能手机屏幕朝上平放在桌子上。在此方向上,我们的坐标系使得重力作用的方向为负\(z\)方向。重力将我们的手机拉向负\(z\)方向,因此我们的加速度计,即使完全静止,也会记录负\(z\)方向上 9.8 \(m/s^2\)的加速度。图 16.3显示了在此方向上手机的加速度计数据。
图 16.3 - 静止状态下的示例加速度计数据
请注意,\(x(t)\)和\(y(t)\)保持恒定为 0,而\(z(t)\)恒定为 -1 g。我们的加速度计记录所有加速度,包括重力加速度。
每个时间序列测量该方向上的总加速度。总加速度是用户加速度和重力加速度的总和。
用户加速度是由于用户移动而导致的设备加速度,当手机完全静止时,它恒定为 0。但是,当用户随身携带设备移动时,用户加速度很少是恒定的,因为人很难以恒定的加速度移动。
图 16.4 - 分量信号
为了计算步数,我们对用户在重力方向上产生的弹跳感兴趣。这意味着我们有兴趣从 3 维加速度信号中分离出描述**重力方向上的用户加速度**的 1 维时间序列(图 16.4)。
在我们的简单示例中,重力加速度在\(x(t)\)和\(z(t)\)中为 0,在\(y(t)\)中恒定为 9.8 \(m/s^2\)。因此,在我们的总加速度图中,\(x(t)\)和\(z(t)\)围绕 0 波动,而\(y(t)\)围绕 -1 g波动。在我们的用户加速度图中,我们注意到,因为我们已经去除了重力加速度,所以所有三个时间序列都围绕 0 波动。请注意\(y_{u}(t)\)中明显的峰值。这些是由于步弹跳造成的!在我们的最后一个图中,重力加速度\(y_{g}(t)\)恒定为 -1 g,而\(x_{g}(t)\)和\(z_{g}(t)\)恒定为 0。
因此,在我们的示例中,我们感兴趣的重力方向上的 1 维用户加速度时间序列是\(y_{u}(t)\)。虽然\(y_{u}(t)\)不像我们的完美正弦波那样平滑,但我们可以识别峰值,并使用这些峰值来计算步数。到目前为止,一切顺利。现在,让我们为我们的世界添加更多现实。
如果一个人将手机放在肩上的包里,手机处于更不稳定的位置会怎样?更糟糕的是,如果手机在步行过程中的一部分时间里在包里旋转,就像图 16.5中那样?
图 16.5 - 更复杂的步行
哎呀。现在所有三个分量都有一个非零的重力加速度,因此重力方向上的用户加速度现在分布在所有三个时间序列中。为了确定重力方向上的用户加速度,我们首先必须确定重力作用的方向。为此,我们必须将每个三个时间序列中的总加速度分成一个用户加速度时间序列和一个重力加速度时间序列(图 16.6)。
图 16.6 - 更复杂的分量信号
然后我们可以分离每个分量中重力方向上的用户加速度部分,从而得到仅重力方向上的用户加速度时间序列。
让我们在下面两步中定义这一点
我们将分别查看每个步骤,并戴上我们的数学家帽子。
我们可以使用一种称为滤波器的工具将总加速度时间序列分成用户加速度时间序列和重力加速度时间序列。
滤波器是信号处理中用于从信号中去除不需要的分量的工具。
低通滤波器允许低频信号通过,同时衰减高于设定阈值的信号。相反,高通滤波器允许高频信号通过,同时衰减低于设定阈值的信号。以音乐为例,低通滤波器可以消除高音,高通滤波器可以消除低音。
在我们的情况下,频率(以 Hz 为单位)表示加速度变化的速度。恒定加速度的频率为 0 Hz,而非恒定加速度的频率为非零值。这意味着我们的恒定重力加速度是 0 Hz 信号,而用户加速度不是。
对于每个分量,我们可以将总加速度通过低通滤波器,这样我们就只剩下重力加速度时间序列了。然后我们可以从总加速度中减去重力加速度,这样我们就得到了用户加速度时间序列(图 16.7)。
图 16.7 - 低通滤波器
滤波器种类繁多。我们将使用的一种称为无限脉冲响应 (IIR) 滤波器。我们选择 IIR 滤波器是因为其开销低且易于实现。我们选择的 IIR 滤波器使用以下公式实现
\[ output_{i} = \alpha_{0}(input_{i}\beta_{0} + input_{i-1}\beta_{1} + input_{i-2}\beta_{2} - output_{i-1}\alpha_{1} - output_{i-2}\alpha_{2}) \]
数字滤波器的设计超出了本章的范围,但有必要进行非常简短的预告讨论。这是一个经过充分研究的迷人话题,具有许多实际应用。可以设计数字滤波器以消除任何所需的频率或频率范围。\(\alpha\)和\(\beta\)公式中的值是系数,根据截止频率和我们想要保留的频率范围设置。
我们希望消除所有频率,除了我们恒定的重力加速度,因此我们选择了衰减高于 0.2 Hz 频率的系数。请注意,我们将阈值设置略高于 0 Hz。虽然重力确实产生了真正的 0 Hz 加速度,但我们真实且不完美的世界拥有真实且不完美的加速度计,因此我们在测量中允许一定的误差范围。
让我们使用之前的示例逐步完成低通滤波器的实现。我们将
我们将重力加速度的前两个值初始化为 0,以便公式具有初始值可以使用。
\[x_{g}(0) = x_{g}(1) = y_{g}(0) = y_{g}(1) = z_{g}(0) = z_{g}(1) = 0\]
然后,我们将为每个时间序列实现滤波器公式。
\[x_{g}(t) = \alpha_{0}(x(t)\beta_{0} + x(t-1)\beta_{1} + x(t-2)\beta_{2} - x_{g}(t-1)\alpha_{1} - x_{g}(t-2)\alpha_{2})\]
\[y_{g}(t) = \alpha_{0}(y(t)\beta_{0} + y(t-1)\beta_{1} + y(t-2)\beta_{2} - y_{g}(t-1)\alpha_{1} - y_{g}(t-2)\alpha_{2})\]
\[z_{g}(t) = \alpha_{0}(z(t)\beta_{0} + z(t-1)\beta_{1} + z(t-2)\beta_{2} - z_{g}(t-1)\alpha_{1} - z_{g}(t-2)\alpha_{2})\]
低通滤波后的结果时间序列在图 16.8中。
图 16.8 - 重力加速度
\(x_{g}(t)\) 和 \(z_{g}(t)\) 徘徊在 0 附近,而 \(y_{g}(t)\) 非常快地下降到 \(-1g\)。 \(y_{g}(t)\) 中的初始 0 值来自公式的初始化。
现在,要计算用户加速度,我们可以从总加速度中减去重力加速度
\[ x_{u}(t) = x(t) - x_{g}(t) \] \[ y_{u}(t) = y(t) - y_{g}(t) \] \[ z_{u}(t) = z(t) - z_{g}(t) \]
结果是在图 16.9中看到的时间序列。我们已成功地将总加速度分解为用户加速度和重力加速度!
图 16.9 - 分解后的加速度
\(x_{u}(t)\)、\(y_{u}(t)\) 和 \(z_{u}(t)\) 包括用户的所有运动,而不仅仅是重力方向上的运动。我们这里的目标是最终得到一个一维时间序列,表示重力方向上的用户加速度。这将包括每个方向上用户加速度的一部分。
让我们开始吧。首先,一些线性代数 101。不要急着把数学家的帽子摘掉!
在处理坐标时,您很快就会遇到点积,它是用于比较\(x\)、\(y\) 和 \(z\) 坐标的大小和方向的基本工具之一。
点积将我们从三维空间带到一维空间(图 16.10)。当我们取两个时间序列(用户加速度和重力加速度)的点积时,这两个时间序列都位于三维空间中,我们将得到一个位于一维空间中的单个时间序列,表示重力方向上用户加速度的一部分。我们将任意地将这个新的时间序列称为 \(a(t)\),因为,嗯,每个重要的时间序列都应该有一个名字。
图 16.10 - 点积
我们可以使用公式 \(a(t) = x_{u}(t)x_{g}(t) + y_{u}(t)y_{g}(t) + z_{u}(t)z_{g}(t)\) 为我们之前的示例实现点积,这将使我们得到位于一维空间中的 \(a(t)\)(图 16.11)。
图 16.11 - 实现点积
现在我们可以直观地找出 \(a(t)\) 中的步数在哪里。点积非常强大,但又非常简单。
我们看到,当我们加入现实世界和真实用户的挑战时,我们看似简单的问题很快就变得更加复杂了。但是,我们离计数步数越来越近了,我们可以看到 \(a(t)\) 已经开始类似于我们理想的正弦波。但是,只是“有点像”开始。我们仍然需要使我们杂乱的 \(a(t)\) 时间序列变得更平滑。 \(a(t)\) 当前状态存在四个主要问题(图 16.12)。让我们检查一下每个问题。
图 16.12 - 跳跃、缓慢、短暂、颠簸
\(a(t)\) 非常“跳跃”,因为手机在每次迈步时都会晃动,从而在我们的时间序列中添加高频分量。这种跳跃性称为噪声。通过研究大量数据集,我们确定步进加速度最大为 5 Hz。我们可以使用低通 IIR 滤波器去除噪声,选择 \(\alpha\) 和 \(\beta\) 以衰减所有高于 5 Hz 的信号。
以 100 的采样率,\(a(t)\) 中显示的缓慢峰值跨越 1.5 秒,这对于步进来说太慢了。在研究了足够数量的数据样本后,我们确定我们能采取的最慢的步进频率为 1 Hz。较慢的加速度是由于低频分量造成的,我们可以再次使用高通 IIR 滤波器去除该分量,将 \(\alpha\) 和 \(\beta\) 设置为消除所有低于 1 Hz 的信号。
当用户使用应用程序或拨打电话时,加速度计会在重力方向上记录微小的运动,在我们的时间序列中表现为短暂的峰值。我们可以通过设置最小阈值来消除这些短暂的峰值,并在 \(a(t)\) 以正方向越过该阈值时计数步数。
我们的计步器应该适应许多具有不同步态的人,因此我们根据大量人群和步态的样本设置了步进频率的最小值和最大值。这意味着我们有时可能会过滤过多或过少。虽然我们通常会得到相当平滑的峰值,但我们有时可能会得到“更颠簸”的峰值。图 16.12 放大了这样一个峰值。
当颠簸发生在我们的阈值处时,我们可能会错误地为一个峰值计算过多的步数。我们将使用一种称为滞后的方法来解决这个问题。滞后是指输出对过去输入的依赖性。我们可以计算正方向上的阈值交叉次数,以及负方向上的 0 交叉次数。然后,我们只计算阈值交叉发生在 0 交叉之后的情况下的步数,确保我们只计算每一步一次。
图 16.13 - 微调后的峰值
在考虑了这四种情况后,我们成功地使我们杂乱的 \(a(t)\) 非常接近我们的理想正弦波(图 16.13),从而使我们能够计算步数。
乍一看,这个问题似乎很简单。然而,现实世界和真实用户给我们带来了几个难题。让我们回顾一下我们如何解决这个问题
作为培训或学术环境中的软件开发人员,我们可能会得到一个完美的信号,并被要求编写代码来计算该信号中的步数。虽然这可能是一个有趣的编码挑战,但它不是我们可以在实际情况中应用的东西。我们看到,在现实中,当加入重力和用户时,问题会变得稍微复杂一些。我们使用数学工具来解决复杂性,并且能够解决现实世界中的问题。现在是时候将我们的解决方案转换为代码了。
本章的目标是创建一个基于 Ruby 的 Web 应用程序,该应用程序接受加速度计数据,解析、处理和分析数据,并返回所走步数、行进距离和经过时间。
我们的解决方案要求我们多次过滤时间序列。与其在整个程序中散布过滤代码,不如创建一个负责过滤的类,如果我们将来需要增强或修改它,我们只需要更改该类即可。这种策略称为关注点分离,这是一种常用的设计原则,它提倡将程序分解成不同的部分,每个部分都有一个主要关注点。这是一种编写干净、可维护且易于扩展的代码的绝佳方式。我们将在本章中多次重新讨论这个想法。
让我们深入研究过滤代码,它逻辑上包含在一个名为Filter的类中。
class Filter
COEFFICIENTS_LOW_0_HZ = {
alpha: [1, -1.979133761292768, 0.979521463540373],
beta: [0.000086384997973502, 0.000172769995947004, 0.000086384997973502]
}
COEFFICIENTS_LOW_5_HZ = {
alpha: [1, -1.80898117793047, 0.827224480562408],
beta: [0.095465967120306, -0.172688631608676, 0.095465967120306]
}
COEFFICIENTS_HIGH_1_HZ = {
alpha: [1, -1.905384612118461, 0.910092542787947],
beta: [0.953986986993339, -1.907503180919730, 0.953986986993339]
}
def self.low_0_hz(data)
filter(data, COEFFICIENTS_LOW_0_HZ)
end
def self.low_5_hz(data)
filter(data, COEFFICIENTS_LOW_5_HZ)
end
def self.high_1_hz(data)
filter(data, COEFFICIENTS_HIGH_1_HZ)
end
private
def self.filter(data, coefficients)
filtered_data = [0,0]
(2..data.length-1).each do |i|
filtered_data << coefficients[:alpha][0] *
(data[i] * coefficients[:beta][0] +
data[i-1] * coefficients[:beta][1] +
data[i-2] * coefficients[:beta][2] -
filtered_data[i-1] * coefficients[:alpha][1] -
filtered_data[i-2] * coefficients[:alpha][2])
end
filtered_data
end
end无论何时我们的程序需要过滤时间序列,我们都可以使用需要过滤的数据调用Filter中的一个类方法
low_0_hz 用于对接近 0 Hz 的信号进行低通滤波low_5_hz 用于对 5 Hz 或以下的信号进行低通滤波high_1_hz 用于对高于 1 Hz 的信号进行高通滤波每个类方法都调用filter,后者实现 IIR 滤波器并返回结果。如果我们希望将来添加更多滤波器,我们只需要更改此类即可。请注意,所有魔法数字都在顶部定义。这使我们的类更易于阅读和理解。
我们的输入数据来自移动设备,例如 Android 手机和 iPhone。当今市场上的大多数手机都内置了加速度计,能够记录总加速度。让我们将记录总加速度的输入数据格式称为组合格式。许多(但不是全部)设备还可以分别记录用户加速度和重力加速度。让我们将此格式称为分离格式。能够以分离格式返回数据的设备必然能够以组合格式返回数据。但是,反过来并不总是成立。有些设备只能以组合格式记录数据。组合格式的输入数据需要通过低通滤波器才能转换为分离格式。
我们希望我们的程序能够处理市场上所有带有加速度计的移动设备,因此我们需要接受两种格式的数据。让我们分别看看我们将要接受的两种格式。
组合格式中的数据是随时间推移的 \(x\)、\(y\) 和 \(z\) 方向上的总加速度。\(x\)、\(y\) 和 \(z\) 值将用逗号分隔,每单位时间的样本将用分号分隔。
\[ x_1,y_1,z_1; \ldots x_n,y_n,z_n; \]
分离格式返回随时间推移的 \(x\)、\(y\) 和 \(z\) 方向上的用户加速度和重力加速度。用户加速度值将用竖线与重力加速度值分隔。
\[ x^{u}_1,y^{u}_1,z^{u}_1 \vert x^{g}_1,y^{g}_1,z^{g}_1; \ldots x^{u}_n,y^{u}_n,z^{u}_n \vert x^{g}_n,y^{g}_n,z^{g}_n; \]
处理多种输入格式是一个常见的编程问题。如果我们希望整个程序都能处理这两种格式,那么处理数据的每一部分代码都需要知道如何处理这两种格式。这很快就会变得非常混乱,尤其是在添加第三种(或第四种、第五种或第一百种)输入格式时。
我们处理这个问题最简洁的方法是,尽快将两种输入格式都转换为标准格式,以便程序的其余部分可以使用这种新的标准格式。我们的解决方案要求我们分别处理用户加速度和重力加速度,因此我们的标准格式需要将两种加速度分开(图 16.14)。
图 16.14 - 标准格式
我们的标准格式允许我们存储时间序列,因为每个元素都表示某一时刻的加速度。我们将其定义为一个三维数组。让我们一层层剥开它。
我们系统的输入将是来自加速度计的数据、步行用户的信息(性别、步幅等)以及步行试验本身的信息(采样率、实际步数等)。我们的系统将应用信号处理解决方案,并输出计算出的步数、实际步数与计算步数之间的差值、行进距离和经过时间。从输入到输出的整个过程可以看作是一个管道(图 16.15)。
图 16.15 - 管道
本着关注分离的原则,我们将分别编写管道中每个不同组件的代码——解析、处理和分析。
鉴于我们希望尽早将数据转换为标准格式,因此编写一个解析器,使我们能够获取两种已知的输入格式并将其转换为标准输出格式作为我们管道的第一部分是有意义的。我们的标准格式将用户加速度和重力加速度分开,这意味着如果我们的数据采用组合格式,我们的解析器将需要先将其通过低通滤波器以转换为标准格式。
图 16.16 - 初始工作流程
将来,如果我们必须添加另一种输入格式,我们唯一需要修改的代码就是这个解析器。让我们再次分离关注点,并创建一个 Parser 类来处理解析。
class Parser
attr_reader :parsed_data
def self.run(data)
parser = Parser.new(data)
parser.parse
parser
end
def initialize(data)
@data = data
end
def parse
@parsed_data = @data.to_s.split(';').map { |x| x.split('|') }
.map { |x| x.map { |x| x.split(',').map(&:to_f) } }
unless @parsed_data.map { |x| x.map(&:length).uniq }.uniq == [[3]]
raise 'Bad Input. Ensure data is properly formatted.'
end
if @parsed_data.first.count == 1
filtered_accl = @parsed_data.map(&:flatten).transpose.map do |total_accl|
grav = Filter.low_0_hz(total_accl)
user = total_accl.zip(grav).map { |a, b| a - b }
[user, grav]
end
@parsed_data = @parsed_data.length.times.map do |i|
user = filtered_accl.map(&:first).map { |elem| elem[i] }
grav = filtered_accl.map(&:last).map { |elem| elem[i] }
[user, grav]
end
end
end
endParser 具有类级别的 run 方法以及一个初始化器。这是一种我们将多次使用的模式,因此值得讨论一下。初始化器通常用于设置对象,不应该做太多工作。Parser 的初始化器仅采用组合格式或分离格式的 data 并将其存储在实例变量 @data 中。parse 实例方法在内部使用 @data,并完成解析的繁重工作,并将标准格式的结果设置为 @parsed_data。在我们的例子中,我们永远不需要在不立即调用 parse 的情况下实例化 Parser 实例。因此,我们添加了一个方便的类级 run 方法,该方法实例化 Parser 的一个实例,在其上调用 parse 并返回对象的实例。现在,我们可以将我们的输入数据传递给 run,知道我们将收到一个 Parser 实例,其中 @parsed_data 已经设置。
让我们看看我们辛勤工作的 parse 方法。此过程的第一步是获取字符串数据并将其转换为数值数据,从而得到一个三维数组。听起来熟悉吧?接下来我们要做的是确保格式符合预期。除非最内层数组的每个数组都恰好有三个元素,否则我们会抛出异常。否则,我们将继续。
请注意此时两种格式的 @parsed_data 之间的区别。在组合格式中,它包含正好一个数组的数组
\[ [[[x_1, y_1, z_1]], \ldots [[x_n, y_n, z_n]] \]
在分离格式中,它包含正好两个数组的数组
\[[[[x_{u}^1,y_{u}^1,z_{u}^1], [x_{g}^1,y_{g}^1,z_{g}^1]], ... [[x_{u}^n,y_{u}^n,z_{u}^n], [x_{g}^n,y_{g}^n,z_{g}^n]]]\]
经过此操作后,分离格式已经处于我们所需的标准格式。太棒了。但是,如果数据是组合的(或者等效地,只有一个数组,而分离格式会有两个),那么我们将继续进行两个循环。第一个循环使用 Filter 的 :low_0_hz 类型将总加速度分解为重力和用户加速度,第二个循环将数据重新组织为标准格式。
parse 将 @parsed_data 保留为标准格式的数据,无论我们最初使用的是组合数据还是分离数据。真是令人欣慰!
随着程序变得越来越复杂,一个改进方向是通过抛出包含更具体错误消息的异常来简化用户的生活,以便他们能够更快地追踪常见的输入格式问题。
根据我们定义的解决方案,在我们可以计算步数之前,我们的代码需要对解析后的数据执行几件事
我们将通过在计步时避免这些峰值来处理短而颠簸的峰值。
现在,我们已经将数据转换为标准格式,我们可以对其进行处理,使其进入可以分析以计数步数的状态(图 16.17)。
图 16.17 - 处理
处理的目的是获取标准格式的数据,并逐步对其进行清理,使其尽可能接近我们理想的正弦波。我们的两个处理操作(获取点积和过滤)是完全不同的,但它们都旨在处理我们的数据,因此我们将创建一个名为 Processor 的类。
class Processor
attr_reader :dot_product_data, :filtered_data
def self.run(data)
processor = Processor.new(data)
processor.dot_product
processor.filter
processor
end
def initialize(data)
@data = data
end
def dot_product
@dot_product_data = @data.map do |x|
x[0][0] * x[1][0] + x[0][1] * x[1][1] + x[0][2] * x[1][2]
end
end
def filter
@filtered_data = Filter.low_5_hz(@dot_product_data)
@filtered_data = Filter.high_1_hz(@filtered_data)
end
end同样,我们看到了 run 和 initialize 方法模式。run 直接调用我们的两个处理器方法 dot_product 和 filter。每个方法都完成我们的两个处理操作之一。dot_product 隔离重力方向上的运动,filter 依次应用低通和高通滤波器以去除跳跃和缓慢的峰值。
如果提供了有关使用计步器的人的信息,我们就可以测量的不止是步数。我们的计步器将测量行进距离和经过时间,以及步数。
移动计步器通常由一个人使用。步行期间的行进距离是通过将所走的步数乘以该人的步幅长度来计算的。如果步幅长度未知,我们可以使用可选的用户信息(如性别和身高)来近似估计。让我们创建一个 User 类来封装这些相关信息。
class User
GENDER = ['male', 'female']
MULTIPLIERS = {'female' => 0.413, 'male' => 0.415}
AVERAGES = {'female' => 70.0, 'male' => 78.0}
attr_reader :gender, :height, :stride
def initialize(gender = nil, height = nil, stride = nil)
@gender = gender.to_s.downcase unless gender.to_s.empty?
@height = Float(height) unless height.to_s.empty?
@stride = Float(stride) unless stride.to_s.empty?
raise 'Invalid gender' if @gender && !GENDER.include?(@gender)
raise 'Invalid height' if @height && (@height <= 0)
raise 'Invalid stride' if @stride && (@stride <= 0)
@stride ||= calculate_stride
end
private
def calculate_stride
if gender && height
MULTIPLIERS[@gender] * height
elsif height
height * (MULTIPLIERS.values.reduce(:+) / MULTIPLIERS.size)
elsif gender
AVERAGES[gender]
else
AVERAGES.values.reduce(:+) / AVERAGES.size
end
end
end在我们的类的顶部,我们定义了一些常量,以避免在整个过程中硬编码魔法数字和字符串。出于本文讨论的目的,让我们假设 MULTIPLIERS 和 AVERAGES 中的值是从大量不同人群的样本中确定的。
我们的初始化器接受 gender、height 和 stride 作为可选参数。如果传递了可选参数,则我们的初始化器会在进行一些数据格式化后设置相同名称的实例变量。对于无效值,我们会抛出异常。
即使提供了所有可选参数,输入步幅也优先。如果未提供,则 calculate_stride 方法将确定对用户而言最准确的步幅长度。这是通过一个 if 语句完成的
MULTIPLIERS 中两个值的平均值。AVERAGES 中的平均步幅长度。AVERAGES 中两个值的平均值,并将其用作我们的步幅。请注意,我们在 if 语句中越往下走,我们的步幅长度就越不准确。无论如何,我们的 User 类都会尽其所能确定步幅长度。
旅行时间是通过将 Processor 的 @parsed_data 中的数据样本数量除以设备的采样率(如果我们有的话)来测量的。由于速率更多地与试验步行本身相关,而不是用户,并且 User 类实际上不必知道采样率,因此现在是创建一个非常小的 Trial 类的好时机。
class Trial
attr_reader :name, :rate, :steps
def initialize(name, rate = nil, steps = nil)
@name = name.to_s.delete(' ')
@rate = Integer(rate.to_s) unless rate.to_s.empty?
@steps = Integer(steps.to_s) unless steps.to_s.empty?
raise 'Invalid name' if @name.empty?
raise 'Invalid rate' if @rate && (@rate <= 0)
raise 'Invalid steps' if @steps && (@steps < 0)
end
endTrial 中的所有属性读取器都在初始化器中根据传递的参数进行设置
name 是特定试验的名称,有助于区分不同的试验。rate 是试验期间加速度计的采样率。steps 用于设置实际步数,以便我们可以记录用户实际步数与程序计算出的步数之间的差异。与我们的 User 类非常相似,某些信息是可选的。如果我们有这些信息,我们将有机会输入试验的详细信息。如果我们没有这些详细信息,我们的程序将绕过计算其他结果,例如旅行时间。与我们的 User 类另一个相似之处是防止无效值。
现在是时候在代码中实现我们的计步策略了。到目前为止,我们有一个 Processor 类,其中包含 @filtered_data,它是代表重力方向上的用户加速度的干净时间序列。我们还有可以提供有关用户和试验必要信息的类。我们缺少的是一种使用 User 和 Trial 中的信息分析 @filtered_data,并计数步数、测量距离和测量时间的方法。
我们程序的分析部分不同于 Processor 的数据操作,也不同于 User 和 Trial 类的信息收集和聚合。让我们创建一个名为 Analyzer 的新类来执行此数据分析。
class Analyzer
THRESHOLD = 0.09
attr_reader :steps, :delta, :distance, :time
def self.run(data, user, trial)
analyzer = Analyzer.new(data, user, trial)
analyzer.measure_steps
analyzer.measure_delta
analyzer.measure_distance
analyzer.measure_time
analyzer
end
def initialize(data, user, trial)
@data = data
@user = user
@trial = trial
end
def measure_steps
@steps = 0
count_steps = true
@data.each_with_index do |data, i|
if (data >= THRESHOLD) && (@data[i-1] < THRESHOLD)
next unless count_steps
@steps += 1
count_steps = false
end
count_steps = true if (data < 0) && (@data[i-1] >= 0)
end
end
def measure_delta
@delta = @steps - @trial.steps if @trial.steps
end
def measure_distance
@distance = @user.stride * @steps
end
def measure_time
@time = @data.count/@trial.rate if @trial.rate
end
end我们在 Analyzer 中做的第一件事是定义一个 THRESHOLD 常量,我们将使用它来避免将短峰值计为步数。出于本文讨论的目的,让我们假设我们已经分析了许多不同的数据集,并确定了一个容纳了最大数量数据集的阈值。最终,阈值可以变得动态化,并根据用户计算出的步数与实际步数而有所不同;如果可以的话,可以使用学习算法。
我们的Analyzer的初始化器接受一个data参数以及User和Trial的实例,并将实例变量@data、@user和@trial设置为传入的参数。run方法调用measure_steps、measure_delta、measure_distance和measure_time。让我们看看每个方法。
measure_steps终于!计步应用的计步部分。我们在measure_steps中首先做的事情是初始化两个变量
@steps用于统计步数。count_steps用于滞后现象,以确定我们是否允许在某个时间点统计步数。然后,我们遍历@processor.filtered_data。如果当前值大于或等于THRESHOLD,并且前一个值小于THRESHOLD,那么我们已经以正方向越过了阈值,这可能表明迈出了一步。如果count_steps为false,则unless语句跳到下一个数据点,表明我们已经为该峰值统计了一步。如果没有,我们将@steps加1,并将count_steps设置为false,以防止为该峰值统计更多步数。下一个if语句在我们的时间序列以负方向越过\(x\)轴后,将count_steps设置为true,然后我们进入下一个峰值。
就是这样,我们程序的计步部分!我们的Processor类做了很多工作来清理时间序列并去除会导致错误计步的频率,因此我们实际的计步实现并不复杂。
值得注意的是,我们将整个步行时间序列存储在内存中。我们的试验都是短距离步行,所以目前这不是问题,但最终我们希望分析具有大量数据的长距离步行。理想情况下,我们希望将数据流式传输进来,只在内存中存储时间序列的非常小的一部分。考虑到这一点,我们已经做了工作来确保我们只需要当前数据点和它之前的数据点。此外,我们使用布尔值实现了滞后现象,因此我们不需要在时间序列中向后查看以确保我们已在0处越过\(x\)轴。
在考虑产品未来可能的迭代和过度设计适用于阳光下所有可能的产品方向的解决方案之间,存在微妙的平衡。在这种情况下,假设我们将在不久的将来不得不处理更长的步行是合理的,并且在计步中考虑这一点的成本相当低。
measure_delta如果试验提供了步行期间实际步数,则measure_delta将返回计算步数和实际步数之间的差值。
measure_distance距离是通过将用户的步幅乘以步数来计算的。由于距离取决于步数,因此必须在measure_distance之前调用measure_steps。
measure_time只要我们有采样率,时间就可以通过将filtered_data中样本的总数除以采样率来计算。因此,时间以秒为单位计算。
我们的Parser、Processor和Analyzer类,虽然各自有用,但肯定在一起更好。我们的程序通常会使用它们来运行我们之前介绍的管道。由于管道需要频繁运行,因此我们将创建一个Pipeline类来为我们运行它。
class Pipeline
attr_reader :data, :user, :trial, :parser, :processor, :analyzer
def self.run(data, user, trial)
pipeline = Pipeline.new(data, user, trial)
pipeline.feed
pipeline
end
def initialize(data, user, trial)
@data = data
@user = user
@trial = trial
end
def feed
@parser = Parser.run(@data)
@processor = Processor.run(@parser.parsed_data)
@analyzer = Analyzer.run(@processor.filtered_data, @user, @trial)
end
end我们使用我们现在熟悉的run模式,并向Pipeline提供加速度计数据以及User和Trial的实例。feed方法实现了管道,它需要使用加速度计数据运行Parser,然后使用解析器的解析数据运行Processor,最后使用处理器的过滤数据运行Analyzer。Pipeline保留@parser、@processor和@analyzer实例变量,以便程序可以通过应用程序访问这些对象的信息以用于显示目的。
我们完成了程序中最费力的部分。接下来,我们将构建一个网络应用程序,以用户喜爱的格式呈现数据。网络应用程序自然地将数据处理与数据呈现分开。在查看代码之前,让我们从用户的角度看看我们的应用程序。
当用户第一次通过导航到/uploads进入应用程序时,他们会看到一个现有数据的表格和一个通过上传加速度计输出文件以及试验和用户信息来提交新数据的表单(图 16.18)。
图 16.18 - 上传视图
提交表单会将数据存储到文件系统,解析、处理和分析它,并重定向回/uploads,并在表格中添加新条目。
点击条目的“详细信息”链接会向用户呈现图 16.19中的以下视图。
图 16.19 - 详细信息视图
呈现的信息包括用户通过上传表单输入的值、程序计算的值以及点积运算后时间序列的图表,以及过滤后的时间序列图表。用户可以使用“返回上传”链接导航回/uploads。
让我们从技术上看看上面概述的功能对我们的意义。我们需要两个我们还没有的主要组件
让我们检查这两个需求中的每一个。
我们的应用程序需要将输入数据存储到文件系统并从文件系统检索数据。我们将创建一个Upload类来执行此操作。由于该类仅处理文件系统,并且与计步器的实现没有直接关系,因此为了简洁起见,我们省略了它,但值得讨论其基本功能。我们的Upload类有三个类级方法用于文件系统的访问和检索,所有这些方法都返回一个或多个Upload实例
create接受一个文件以及用户和试验信息。它将文件存储到文件系统,存储在它生成的包含用户和试验信息的文件名下。@file_path、@user和@trial实例变量分别允许访问文件路径、用户对象和试验对象。find接受一个文件路径并返回一个Upload实例。all返回一个Upload实例数组,每个文件系统中的加速度计数据文件对应一个实例。再次,我们明智地将程序中的关注点分开了。所有与存储和检索相关的代码都包含在Upload类中。随着应用程序的增长,我们可能希望使用数据库而不是将所有内容保存到文件系统。当需要这样做时,我们只需更改Upload类即可。这使我们的重构变得简单而干净。
将来,我们可以将User和Trial对象保存到数据库中。然后,Upload中的create、find和all方法也将与User和Trial相关。这意味着我们可能会将它们重构到自己的类中,以处理一般的数据存储和检索,并且我们的每个User、Trial和Upload类都将继承自该类。我们最终可能会向该类添加辅助查询方法,并从那里继续构建它。
网络应用程序已经构建了很多次,因此我们将利用开源社区的重要工作,并使用现有的框架为我们完成乏味的管道工作。Sinatra 框架就是这样做的。用该工具自己的话说,Sinatra 是“一个用于在 Ruby 中快速创建 Web 应用程序的 DSL”。完美。
我们的网络应用程序需要响应 HTTP 请求,因此我们需要一个文件,为每个 HTTP 方法和 URL 的组合定义一个路由和关联的代码块。让我们将其命名为pedometer.rb。
get '/uploads' do
@error = "A #{params[:error]} error has occurred." if params[:error]
@pipelines = Upload.all.inject([]) do |a, upload|
a << Pipeline.run(File.read(upload.file_path), upload.user, upload.trial)
a
end
erb :uploads
end
get '/upload/*' do |file_path|
upload = Upload.find(file_path)
@pipeline = Pipeline.run(File.read(file_path), upload.user, upload.trial)
erb :upload
end
post '/create' do
begin
Upload.create(params[:data][:tempfile], params[:user], params[:trial])
redirect '/uploads'
rescue Exception => e
redirect '/uploads?error=creation'
end
endpedometer.rb允许我们的应用程序响应每个路由的 HTTP 请求。每个路由的代码块都通过Upload从文件系统检索数据或将数据存储到文件系统,然后呈现视图或重定向。实例化的实例变量将直接在我们的视图中使用。视图只是显示数据,而不是我们应用程序的重点,因此我们将本节中省略它们的代码。
让我们分别看看pedometer.rb中的每个路由。
GET /uploads导航到https://:4567/uploads会向我们的应用程序发送 HTTP GET 请求,触发我们的get '/uploads'代码。该代码对文件系统中的所有上传运行管道,并呈现uploads视图,该视图显示上传列表和一个提交新上传的表单。如果包含错误参数,则会创建一个错误字符串,并且uploads视图将显示错误。
GET /upload/*点击每个上传的“详细信息”链接会向/upload发送 HTTP GET 请求,并附带该上传的文件路径。管道运行,并呈现upload视图。该视图显示上传的详细信息,包括使用名为 HighCharts 的 JavaScript 库创建的图表。
POST /create我们的最后一个路由,对create的 HTTP POST 请求,是在用户提交uploads视图中的表单时调用的。代码块使用params哈希创建一个新的Upload,使用该哈希从用户通过表单输入的值中获取值,并重定向回/uploads。如果在创建过程中发生错误,则重定向到/uploads会包含一个错误参数,以告知用户某些操作出错。
瞧!我们构建了一个功能齐全的应用程序,具有真正的适用性。
现实世界为我们带来了错综复杂、复杂的挑战。软件能够以最少的资源大规模地解决这些挑战。作为软件工程师,我们有能力在我们的家庭、社区和世界中创造积极的改变。我们的培训,无论是在学术上还是其他方面,都可能使我们具备了编写代码来解决孤立的、定义明确的问题的解决问题的能力。随着我们成长和磨练我们的技艺,我们有责任将这种培训扩展到解决实际问题,这些问题与我们世界的混乱现实交织在一起。我希望本章让您体验到如何将一个实际问题分解成小的、可解决的部分,以及编写优美、简洁、可扩展的代码来构建解决方案。
为在无限精彩的世界中解决有趣的问题干杯。